Bài giảng Trình biên dịch - Chương 3: Phân tích từ vựng

CHệễNG 3
PHAÂN TÍCH Tệỉ VệẽNG 
3.1. Vai troứ cuaỷ boọ phaõn tớch tửứ vửùng
1. Token, maóu, trũ tửứ vửùng
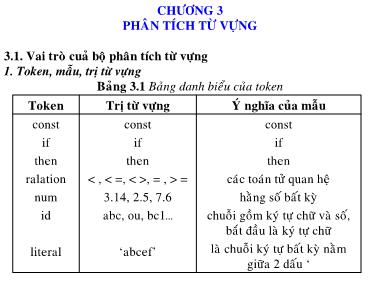
Baỷng 3.1 Baỷng danh bieồu cuỷa token
Token Trũ tửứ vửùng YÙ nghúa cuỷa maóu
const
if
then
ralation
num
id
literal
const
if
then
, = , > =
3.14, 2.5, 7.6
abc, ou, bc1
‘abcef’
const
if
then
caực toaựn tửỷ quan heọ
haống soỏ baỏt kyứ
chuoói goàm kyự tửù chửừ vaứ soỏ, 
baột ủaàu laứ kyự tửù chửừ
laứ chuoói kyự tửù baỏt kyứ naốm
giửừa 2 daỏu ‘
Hỡnh 3.1. Sửù giao tieỏp giửừa boọ phaõn tớch tửứ vửùng vaứ boọ phaõn tớch
cuự phaựp
3.2. CAÙC TÍNH CHAÁT CUÛA TOKEN
3.3. CHệÙA TAẽM CHệễNG TRèNH NGUOÀN
1. Caởp boọ ủeọm
Caỏu taùo
Boọ phaõn tớch
tửứ vửùng
Baỷng danh bieồu
Boọ phaõn
tớch CP
Chửụng trỡnh
nguoàn token
yeõu caàu token
A : = B * . - 2 eof
p1 p2
Hỡnh 3.2. Caởp boọ ủeọm
Quy trỡnh hoaùt ủoọng
Giaỷi thuaọt:
if p2 ụỷ ranh giụựi moọt nửỷa boọ ủeọm then
begin laỏp ủaày N kyự hieọu nhaọp mụựi vaứo nửỷa beõn phaỷi
p2 := p2 + 1;
end 
else if p2 ụỷ taọn cuứng beõn phaỷi boọ ủeọm then 
begin laỏp ủaày N kyứ hieọu nhaọp vaứo nửỷa beõn traựi boọ ủeọm
chuyeồn
p2 veà kyự tửù taọn cuứng beõn traựi cuỷa boọ ủeọm end
else p2 := p2 + 1;
2. Phửụng phaựp caàm canh
A : = B * X EOF - 2 EOF EOF
N kyự tửù N kyự tửù
p1 p2
Hỡnh 3.3. Caởp boọ ủeọm theo phửụng phaựp caàm canh
Giaỷi thuaọt:
p2 := p2 + 1;
if p2 ^ eof then 
if p2 ụỷ ranh giụựi moọt nửỷa boọ ủeọm then 
begin
chaỏt ủaày N kyứ hieọu nhaọp vaứo nửỷa beõn phaỷi boọ ủeọm; 
p2 := p2 + 1 
end
else if p2 ụỷ taọn cuứng beõn phaỷi boọ ủeọm then 
begin
laỏp ủaày N kyự hieọu vaứo nửỷ beõn traựi boọ ủeọm; chuyeồn p2 
veà ủaàu boọ ủeọm
end
else /* dửứng sửù phaõn tớch tửứ vửùng */
3.4. ẹaởc taỷ token
Caực quy taộc ủũnh nghiaừ bieồu thửực chớnh quy
1. ∈ laứ bieồu thửực chớnh quy, bieồu thũ cho taọp {∈}
2. a laứ kyự hieọu thuoọc Σ, bieồu thũ cho taọp {a}
3. r vaứ s laứ hai bieồu thửực chớnh quy, bieồu thũ cho L (r) vaứ L (s) thỡ:
ứ a) (r) | (s) laứ bieồu thửực chớnh quy, bieồu thũ cho L(r) ∪ L(s).
b) (r) (s) laứ bieồu thửực chớnh quy, bieồu thũ cho L(r) L(s).
c) (r)* laứ bieồu thửực chớnh quy, bieồu thũ cho (L(r))*.
d) r laứ bieồu thửực chớnh quy, bieồu thũ cho L(r).
Thớ duù 3.1. Cho Σ = {a, b}
1. a|b 
2. (a| b) | (b| a) 
3. a*
Hai bieồu thửực chớnh quy tửụng ủửụng r vaứ s, kyự hieọu r = s.
2. ẹũnh nghúa chớnh quy
Neỏu Σ laứ taọp kyự hieọu caờn baỷn, thỡ ủũnh nghiaừ chớnh quy laứ chuoói ủũnh
nghiaừ coự daùng: d1→ r1
dn→ rn
Thớ duù 3.2. letter → A | B | |Z | a| b || z
digit → 0 |1| | 9
id→ letter ( letter | digit)*
Thớ duù 3.3. digit→ 0 | 1 | | 9 
digits → digit digit*
optional_fraction → .digits | ∈
optional_exponent → (E (+| - |∈) digits) | ∈
3.5. Nhaọn daùng token
Thớ duù 3.4. Cho vaờn phaùm G:
stmt→ if exp then stmt 
| if exp then stmt else stmt 
| ∈
exp → term relop term | term
term → id | num
ẹũnh nghúa chớnh quy
if → if then → then else→ else 
relop → | >= | | = 
id → letter (letter | digit)* 
num → digit+ (.digit+ | ∈) ( E ( + | - | ∈) digit+ | ∈ )
delim→ blank | tab | newline
ws → delim+
Tửứ ủũnh nghúa chớnh quy ta xaõy dửùng baỷng maóu cho token nhử ụỷ baỷng
3.3 trang 74.
3.6. Sụ ủoà dũch
1. Mieõu taỷ
0 7
8
Baột ủaàu >
=
other
2
3
Start < = return (relop, LE)
6 7
8
> return (relop, NE)
4 return (relop, LT)
5
=
return (relop, EQ)
>
other
6 Hỡnh 3.4. Sụ ủoà dũch cho >= 
vaứ =
0 1
=
other
(relop, EQ)
return (relop, EQ)
*
*
*
Hỡnh 3.5. Sụ ủoà dũch nhaọn daùng token relop
Lửu yự: 
- Phaàn khai baựo bao goàm khai baựo haống, bieỏn bieồu thũ vaứ caực ủũnh
nghúa chớnh quy.
- Phaàn quy taộc bieõn dũch laứ caực phaựt bieồu coự daùng:
p1→ {haứnh vi ngửừ nghúa 1}
p2→ {haứnh vi ngửừ nghúa 2}
pn → {haứnh vi ngửừ nghúa n}
3.8. Automat hửừu haùn
1. Automat hửừu haùn khoõng taỏt ủũnh (NFA)
Thớ duù: Cho NFA: 
Taọp traùng thaựi S = {0, 1,2, 3}; Σ = {a, b}; Traùng thaựi baột ủaàu so = 0; 
Taọp traùng thaựi keỏt thuực F = {3}. 
Baỷng 3.4. Baỷng truyeàn cho NFA ụỷ hỡnh 3.10
Kyự hieọu nhaọp
Traùng thaựi
a b
0 {0, 1} {0}
1 - {2}
2 - {3}
NFA chaỏp nhaọn moọt chuoói nhaọp x neỏu vaứ chổ neỏu toàn taùi moọt ủửụứng
naứo ủoự trong sụ ủoà tửứ traùng thaựi baột ủaàu ủeỏn traùng thaựi keỏt thuực sao
cho taỏt caỷ teõn cuỷa caực caùnh con ủửụứng cho chuoói x. NFA chaỏp nhaọn
chuoói aabb.
2. Automat hửừu haùn taỏt ủũnh (DFA)
DFA laứ trửụứng hụùp ủaởc bieọt cuỷa NFA, noự khoõng coự:
i) Sửù truyeàn roóng.
ii) Vụựi moói traùng thaựi s vaứ kyự hieọu nhaọp a chổ toàn taùi nhieàu nhaỏt moọt
caùnh coự teõn a xuaỏt phaựt tử ứs.
Giaỷi thuaọt 3.1.Moõ phoỷng hoaùt ủoọng cuỷa DFA treõn chuoói nhaọp x.
Thớ duù 3.5
start
30 a 0
a b b1 1
Hỡnh 3.12. DFA nhaọn daùng ngoõn ngửừ (a | b)*abb
3. Chuyeồn NFA sang DFA
Giaỷi thuaọt 3.2. Xaõy dửùng taọp con (Taùo DFA tửứ NFA).
Nhaọp: Cho NFA goùi laứ N.
Xuaỏt: DFA goùi laứ D, nhaọn daùng cuứng ngoõn ngửừ nhử NFA.
Phửụng phaựp: Xaõy dửùng baỷng truyeàn cho D. Moói traùng thaựi cuỷa D laứ
taọp traùng thaựi cuỷa N. D moõ phoỷng ủoàng thụứi moùi chuyeồn ủoọng cuỷa N 
treõn chuoói nhaọp cho trửụực baống caực taực vuù:
∈-closure (s); ∈-closure (T); move (T, a)
Moõ phoỷng 3.2. Xaõy dửùng taọp con
Giaỷi thuaọt: Tớnh ∈-closure
ẹaồy taỏt caỷ caực traùng thaựi trong T leõn stack; Khụỷi taùo ∈-closure (T) 
cho T.
Moõ phoỷng 3.3. Tớnh ∈-closure
Thớ duù 3.6. (H.3.13 ) laứ NFA nhaọn daùng ngoõn ngửừ (a | b )* abb. Chuựng
ta duứng giaỷi thuaọt 3.2 ủeồ xaõy dửùng DFA tửụng ủửụng.
0start
∈
1 10
4∈
a
b
b
a
2
8
3
5
6 7 9
∈
∈
∈
Hỡnh 3.13. NFA nhaọn daùng (a | b)* abb
b
3.9. Tửứ bieồu thửực chớnh quy ủeỏn NFA
Xaõy dửùng NFA tửứ bieồu thửực chớnh quy
Giaỷi thuaọt 3.3. Xaõy dửùng NFA tửứ bieồu thửực chớnh quy (Caỏu truực
Thompson’)
Nhaọp: Bieồu thửực chớnh quy r treõn Σ.
Xuaỏt: NFA nhaọn daùng ngoõn ngửừ L (r).
Phửụng phaựp:
Quy taộc:
1. Vụựi ∈ , xaõy dửùng NFA
2. Vụựi a thuoọc Σ, xaõy dửùng NFA
start
i f
∈
start
i f
a
3. Giaỷ sửỷ N( s ) vaứN( t ) laứ NFA cho bieồu thửực chớnh quy s vaứ t
- Vụựi s | t xaõy dửùng NFA hoón hụùp N (s| t)
i
start f
∈N(s)
N(t) ∈∈
∈
- Vụựi bieồu thửực st, xaõy dửùng NFA hoón hụùp N (st)
start
i f
N(t)N(s)
- Vụựi bieồu thửực s* , xaõy dửùng NFA N (s*)
start
i f
∈
∈
∈
∈
- Bieồu thửực s thỡ N (s) laứ NFA nhaọn daùng L (s)
Caực tớnh chaỏt cuaỷ NFA xaõy dửùng theo caỏu truực Thompson’
Thớ duù 3.7.
Giaỷi thuaọt 3.4. Moõ phoỷng NFA
Nhaọp: NFA goùi laứ N ủửụùc xaõy dửùng theo giaỷi thuaọt 3.3, chuoói nhaọp x. 
X ủửụùc keỏt thuực baống eof, N coự traùng thai baột ủaàu s0 vaứ taọp traùng thaựi
keỏt thuực F.
Xuaỏt: Giaỷi thuaọt traỷ lụứi ủuựng neỏu N chaỏp nhaọn x, ngửụùc laùi traỷ lụứi sai
Phửụng phaựp:
Giaỷi thuaọt: Moõ phoỷng 3.4.
Thớ duù 3.8. Giaỷ sửỷ ta coự NFA ụỷ (H.3.13 ), x laứ chuoói nhaọp chửựa a. 
Duứng giaỷi thuaọt 3.4 xeựt xem NFA coự chaỏp nhaọn x ?. Keỏt quỷa giaỷi thuaọt
traỷ lụứi sai ( nghiaừ laứ a khoõng thuoọc ngoõn ngửừ do NFA nhaọn daùng
Thụứi gian vaứ khoõng gian caàn thieỏt cho vieọc nhaọn daùng moọt chuoói nhaọp:
- ẹoỏi vụựi DFA: khoõng gian O (2 ( )) vaứ thụứi gian O (|x | ).
- ẹoỏi vụựi NFA: khoõng gian O (|r | ) vaứ thụứi gian O (| r | * | x | ).
3.10. Xaõy dửùng DFA trửùc tieỏp tửứ bieồu thửực chớnh quy vaứ vaỏn ủeà toỏi
ửu hoựa vieọc so truứng maóu
1. Traùng thaựi quan troùng cuỷa NFA
Traùng thaựi quan troùng laứ tửứ noự coự sửù truyeàn khaực roóng. Nhử vaọy neỏu
hai taọp traùng thaựi coự cuứng soỏ traùng thaựi quan troùng thỡ chuựng ủửụùc
ủoàng nhaỏt. NFA ủửụùc xaõy dửùng theo caỏu truực Thompson’ coự traùng thaựi
keỏt thuực khoõng coự sửù truyeàn ra, nhử vaọy noự khoõng phaỷi laứ traùng thaựi
quan troùng ( nhửng thửùc sửù noự laùi raỏt quan troùng ). ẹeồ traựnh tỡnh traùng
naứy ngửụứi ta theõm kyự hieọu # vaứo sau bieồu thửực chớnh quy, vaứ traùng
thaựi keỏt thuực coự sửù truyeàn treõn kyự hieọu #. Khi xaõy dửùng taọp con hoaứn
taỏt thỡ traùng thaựi naứo coự sửù truyeàn treõn # laứ traùng thaựi chaỏp nhaọn.
- Bieồu thửực r# ủửụùc goùi laứ bieồu thửực chớnh quy gia toỏ.
Vaờn phaùm cuỷa bieồu thửực chớnh quy:
exp → exp | term exp → term term → term • factor
term → factor factor → factor* factor → ( exp )
factor → a factor → b
Hỡnh 3.16. Caõy phaõn raừ cuỷa bieồu thửực gia toỏ (a| b )* abb#
a
3
b
4
#
6b
5
a
1
b
2
*
• •
• •
Hỡnh 3.17. NFA ủửụùc xaõy dửùng tửứ ( a| b )* abb#
Lửu yự:
- Caực traùng thaựi ủửụùc kyự hieọu baống soỏ laứ traùng thaựi quan troùng; Caực
traùng thaựi ủửụùc kyự hieọu baống chửừ laứ traùng thaựi khoõng quan troùng.
- ễÛ thớ duù 3.6 traùng thaựi A vaứ C coự cuứng soỏ traùng thaựi quan troùng laứ
2,4,7 , trong (H 3.17) laứ 1,2,3:
A = {0,1,2,4,7} C = {1,2,4,5,7}
Astart
∈
B F
2∈
a
#
b
a
1
4
C
D
F 3 6
∈
∈
∈ b4 ba
∈
∈
∈
Baỷng 3.6. Caực quy taộc ủeồ tớnh ba haứm nullable, firstpos, lastpos
Nuựt n nullable (n) firstpos (n) lastpos (n)
n laứ nuựt coự teõn
laứ ∈
true
n laứ nuựt coự teõn
laứ vũ trớ i false {i} {i}
nullable(c1) or
nullable(c2)
firstpos(c1) ∪
firstpos(c2)
lastpos(c1) ∪
lastpos(c2)
nullable(c1) and
nullable(c2)
if nullable(c1) 
then firstpos(c1) ∪
firstpos(c2) 
else firstpos(c1)
if nullable(c2) 
then lastpos(c1) ∪ lastpos(c2) 
else lastpos(c2)
true firstpos(c1) lastpos(c1)
n
c2c1
|
c2c1
° n
c1
∗ n
Caực quy taộc tớnh haứm followpos (n):
1. Neỏu nuựt n laứ nuựt cat vụựi con beõn traựi laứ c1, con beõn phaỷi laứ c2 vaứ i laứ
vũ trớ trong lastpos(c1), thỡ taỏt caỷ vũ trớ trong first(c2) seừ cho vaứo
followpos(i).
2. Neỏu n laứ nuựt star vaứ i laứ vũ trớ trong lastpos(n) thỡ taỏt caỷ caực vũ trớ
trong firstpos(n) seừ cho vaứo followpos(i).
Thớ duù 3.10. Ta xaực ủũnh DFA cho bieồọu thửực (a | b)* abb
{1}a {1} {2}a {2}
# {6}
∗
{1,2} {1,2}
{1,2} {1,2}
{5}a{5}
{4}a{4}
{3}a{3}
{1,2,3}
{1,2,3} {1,2,3}
{1,2,3}
{3}
{4} {5}
{6}
{6}
Hỡnh 3.19. Tớnh caực haứm nullable, firstpos, lastpos cho caực nuựt treõn caõy
phaõn tớch cuỷa bieồu thửực ( a| b )* abb
Sau ủoự ta tớnh haứm followpos.
Baỷng 3.7. caực trũ followpos cuỷa caực nuựt treõn caõy ụỷ (H.3.19) 
Nuựt followpos
1 {1,2,3}
2 {1,2,3}
3 {4}
4 {5} 
5 {6} 
6 _
Giaỷi thuaọt 3.5. Xaõy dửùng DFA tửứ bieồu thửực chớnh quy
Nhaọp: Bieồu thửực chớnh quy r.
Xuaỏt: DFA goùi laứ D, nhaọn daùng ngoõn ngửừ L( r)
Phửụng phaựp :1. Xaõy dửùng caõy phaõn tớch cho BTCQ gia toỏ r#.
2. Tớnh caực haứm nullable, firstpos, lastpos vaứ followpos cho caực nuựt
treõn caõy phaõn tớch
3. Xaõy dửùng caực traùng thaựi, haứm truyeàn vaứ baỷng truyeàn cho D baống
thuỷ tuùc ụỷ (moõ phoỷng 3.5).
Thuỷ tuùc taùo taọp con laứ caực traùng thaựi cuỷa DFA:
Luực ủaàu D chổ coự moọt traùng thaựi baột ủaàu laứ firstpos(root) , chửa ủửụùc
ủaựnh daỏu.
Moõ phoỷng 3.5. Thuỷ tuùc taùo taọp con
while coự traùng thaựi T chửa ủửụùc ủaựnh daỏu, trong taọp traùng thaựi
cuỷa D do begin ủaựnh daỏu T;
for vụựi moói kyự hieọu nhaọp a do;
begin vụựi U laứ taọp caực vũ trớ trong followpos (p), p laứ vũ trớ trong
T, sao cho kyự hieọu taùi vũ trớ p laứ a;
if U khoõng roóng vaứ chửa coự trong taọp traùng thaựi cuỷa D
then begin theõm U vaứo taọp traùng thaựi cuỷa D vaứ laứ traùng thaựi
chửa ủửụùc ủaựnh daỏu;
D[T, a] := U;
end;
end;
end;
Lửu yự: traùng thaựi keỏt thuực cuỷa D coự chửựa vũ trớ cuỷa y.
Thớ duù 3.10. Xaõy dửùng DFA tửứ btcq ( a| b )* abb. (trang 103 -104)
3. Toỏi thieồu soỏ traùng thaựi cuỷa DFA
- Khaựi nieọm DFA ủaày ủuỷ, traùng taựi cheỏt d.
- Chuoói w phaõn bieọt traùng thaựi s vụựi traùng thaựi t.
Thớ duù: DFA ụỷ (H.3.14, tr. 90), neỏu xuaỏt phaựt tửứ C ủeồ nhaọn daùng w=bb 
thỡ khoõng ủi ủửụùc ủeỏn traùng thaựi chaỏp nhaọn, ngửụùc laùi tửứ B thỡ ủi ủeỏn E 
laứ traùng thaựi chaỏp nhaọn.
Giaỷi thuaọt 3.6. Toỏi thieồu soỏ traùng thaựi cuỷa DFA.
Nhaọp: DFA, goùi laứ M coự S, Σ, s0, F. M laứ DFA ủaày ủuỷ.
Xuaỏt: DFA, goùi laứ M’ chaỏp nhaọn ngoõn ngửừ nhử M, vụựi soỏ traùng thaựi
nhoỷ nhaỏt.
Phửụng phaựp: 
1.Taùo Π khụỷi ủaàu coự 2 nhoựm: caực traùng thaựi keỏt thuực F, vaứ caực traùng
thaựi khoõng keỏt thuực S – F.
2. AÙp duùng thuỷ tuùc (moõ phoỷng 3.6) ủeồ taùo Πnew .
3. Neỏu Πnew = Π thỡ Πfinal = Π, tieỏp tuùc bửụực 4, ngửụùc laùi laởp laùi bửụực
2, vụựi Π = Πnew
4. Chuựng ta choùn moói nhoựm 1 traùng thaựi ủaùi dieọn vaứ ủoự laứ traùng thaựi
cuỷa M’ .
5. Neỏu M’ coự traùng thaựi cheỏt d thỡ loaùi noự ra khoỷi M’. Taỏt caỷ caực sửù
truyeàn ủeỏn traùng thaựi d ủeàu khoõng xaực ủũnh.
Moõ phoỷng 3.6. Giaỷi thuaọt taùo Πnew
for vụựi moói nhoựm G cuỷa Π do begin
- chia G thaứnh caực nhoựm nhoỷ hụn sao cho hai traùng thaựi s vaứ t 
cuỷa G seừ ụỷ cuứng moọt nhoựm nhoỷ hụn neỏu vaứ chổ neỏu caực sửù truyeàn treõn
taỏt caỷ caực kyự hieọu nhaọp a tửứ s vaứ t ủeàu ủi ủeỏn caực traùng thaựi keỏ tieỏp ụỷ
trong cuứng moọt nhoựm cuỷa Π;
- ta thay G baống caực nhoựm nhoỷ hụn vửứa ủửụùc taùo neõn, cho
chuựng vaứo Πnew ;
end; 
Thớ duù 3.11. Cho DFA nhử ụỷ (H. 3.14, tr. 90).
Caựch giaỷi ụỷ tr. 106 – 107.
4. Caực phửụng phaựp neựn baỷng truyeàn FA
1. Thu giaỷm haứng vaứ coọt dử thửứa
Hỡnh 3.21. Baỷng truyeàn ủửụùc neựn baống phửụng phaựp thu giaỷm haứng vaứ
coọt dử thửứa
0 – 0 1 0000 222222222 0 – 0 3 0 – 0 
0
1
2
3
4
4
0 0 -1 3 1 -1
1 1 -1 2 1 5
2 2 -1 -1 2 5
3 3 -1 -1 2 -1
4 4 -1 -1 -2 -1
5 4 -1 -1 4 -1
0 1 2 3
yrmap
y next
2. Neựn caởp
Hỡnh 3.22. Baỷng truyeàn neựn theo phửụng phaựp neựn caởp
0 • 7 ‘0’,3 ‘0’,1 ‘1’,1 ‘2’,1 ‘3’,1 ‘4’,2 ‘5’,2 ynext 0
1 • 0 -1-112-1..1111111111-1-1 5-1 ynext 1
2 • 6 ‘0’,2 ‘1’,2 ‘2’,3 ‘3’,4 ‘4’,1 ‘5’,1 ynext 2
3 • 7 ‘0’,1 ‘1’,1 ‘2’,2 ‘3’,2 ‘4’,2 ‘5’,2 ‘6’,2 ynext 3
4 • 7 ‘0’,4 ‘1’,4 ‘2’,4 ‘3’,2 ‘4’,2 ‘5’,2 ‘6’,2 ynext 4
5 • 6 ‘0’,2 ‘1’,2 ‘2’,2 ‘3’,2 ‘4’,1 ‘5’,1 ynext 5
ynext
Moõ phoỷng 3.7. Giaỷi thuaọt tỡm traùng thaựi keỏ tieỏp treõn baỷng truyeàn ủaừ
ủửụùc neựn
row := ynext [t];
I := row^[0], /* row^ laứ ma traọn 1 chieàu ynext t */
if I = 0 then
begin c := ord (a)
s := row^[c]; /* s laứ traùng thaựi keỏ tieỏp */
end
else begin
while (a row^ [i]. chart) and (i < I) do
i := i + 1;
if a = row^[i]. chart then s := row^[i]. State
else writen (‘sai – loói tửứ vửùng’);
end;
3.11. Thieỏt keỏ boọ sinh boọ phaõn tớch tửứ vửùng
Hỡnh 3.23. Trỡnh bieõn dũch Lex vaứ Boọ phaõn tớch tửứ vửùng
Chửụng trỡnh moõ phoỷng FA vaứ
baỷng truyeànTrỡnh bieõn dũch
Lex
a)
Chửụng trỡnh
moõ phoỷng FA
Baỷng truyeàn
b)
ẹaởc taỷ lex
Boọ ủeọm nhaọp
1. Maóu so truứng treõn cụ sụỷ NFA
Hỡnh 3.24. NFA ủửụùc tao ra tửứ sửù ủaởc taỷ LEX
so N(pi)
∈
∈
N(p1)
N(pn)
∈