Bài giảng Đại số tuyến tính - Bài 3: Ma trận nghịch đảo

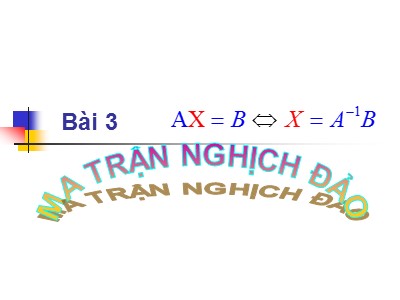
 Bài 3 
MA TRẬN NGHỊCH ĐẢO 
§3: Ma trận nghịch đảo 
§3: Ma trận nghịch đảo 
§3: Ma trận nghịch đảo 
Nhận xét: 
§3: Ma trận nghịch đảo 
Nhận xét: 
§3: Ma trận nghịch đảo 
Tính chất: 
1) 
§3: Ma trận nghịch đảo 
§3: Ma trận nghịch đảo 
§3: Ma trận nghịch đảo 
§3: Ma trận nghịch đảo 
Ví dụ: Tìm ma trận phụ hợp của ma trận sau: 
28 
14 
-6 
-29 
-5 
13 
-12 
-6 
8 
§3: Ma trận nghịch đảo 
Bài tập: Tìm ma trận phụ hợp của ma trận sau: 
-1 
 5 
17 
 0 
-2 
-8 
 0 
 0 
 2 
§3: Ma trận nghịch đảo 
§3: Ma trận nghịch đảo 
Ví dụ: 
§3: Ma trận nghịch đảo 
§3: Ma trận nghịch đảo 
Ví dụ: Tìm ma trận nghịch đảo của ma trận sau: 
§3: Ma trận nghịch đảo 
Ví dụ: Tìm ma trận nghịch đảo của ma trận sau: 
§3: Ma trận nghịch đảo 
Bài tập: Tìm ma trận nghịch đảo của ma trận sau: 
§3: Ma trận nghịch đảo 
Đáp số: 
§3: Ma trận nghịch đảo 
Bài tập: Tìm ma trận nghịch đảo của ma trận sau: 
Chú ý: Đối với ma trận vuông cấp 2 
Đáp số: 
a.Các phép biến đổi sơ cấp (bđsc) trên ma trận: 
§3: Ma trận nghịch đảo 
Tìm ma trận nghịch đảo bằng phương 
pháp Gauss: 
Nhân một số khác không với một hàng (cột) của ma trận. Ký hiệu: 
Đổi chỗ hai hàng (cột) của ma trận. Ký hiệu: 
Cộng vào một hàng (cột) với một hàng (cột) khác đã nhân thêm một số khác không. Ký hiệu: 
Ví dụ: Tìm ma trận nghịch đảo của 
§3: Ma trận nghịch đảo 
Tìm ma trận nghịch đảo bằng phương 
pháp Gauss: 
 bđsc 
b. Phương pháp Gauss: 
Ví dụ: 
§3: Ma trận nghịch đảo 
b. Phương pháp Gauss: 
§3: Ma trận nghịch đảo 
b. Phương pháp Gauss: 
Ví dụ: 
Vậy 
§3: Ma trận nghịch đảo 
Bài toán: Tìm ma trận X thỏa mãn 
 1)	 AX = B 
 2)	XA = B 
 3)	AXB = C 
 4)	AX + kB = C 
§3: Ma trận nghịch đảo 
Ta có: 
§3: Ma trận nghịch đảo 
Ta có: 
§3: Ma trận nghịch đảo 
Ví dụ: Tìm ma trận X thỏa mãn: 
Phương trình có dạng: AX=B 
Ta có: 
§3: Ma trận nghịch đảo 
Vậy 
§3: Ma trận nghịch đảo 
Ví dụ: Tìm ma trận X thỏa mãn: 
Phương trình có dạng 
§3: Ma trận nghịch đảo 
Ta có 
Với nên 
§3: Ma trận nghịch đảo 
Bài tập: Tìm ma trận X thỏa mãn: 
Phương trình có dạng 
§3: Ma trận nghịch đảo 
Bài tập: Tìm ma trận X thỏa mãn: 
Phương trình có dạng