Bài giảng Đại số tuyến tính - Bài 2: Định thức

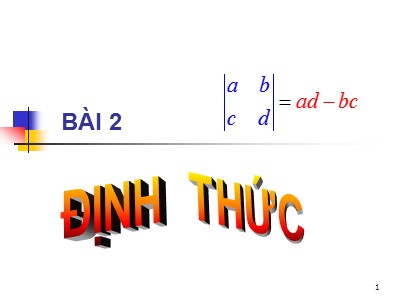
1 
 BÀI 2 
ĐỊNH THỨC 
§2 : Định Thức 
1. Với mỗi ma trận vuông A cấp n 
tồn tại một số thực được gọi là định thức của 
ma trận A, được ký hiệu 
3 
Định thức cấp 2: 
§2: Định Thức 
Ví dụ: 
4 
Định thức cấp 3: 
§2: Định Thức 
5 
Ví dụ: Tính 
§2: Định Thức 
( 1.4.6 
+ 3.2.1 
+ 3.2.5 ) 
-( 3.4.3 
+ 1.1.5 ) 
+ 6.2.2 
=( 24 + 6 + 30 )-( 36 + 24+ 5 )=60-65=-5 
6 
§2: Định Thức 
Bài tập: Tính 
=[ 3.(-2).7+6.1.0+4.5.(-1) ] 
-[ 4.(-2).6+7.1.5+3.0.(-1) ] 
= -62+13= - 49 
7 
§2: Định Thức 
Ví dụ: Tính 
=[2.4.(-2) 
+1.0.3 
+5.(-1).6] 
-[5.4.3 
 +2.0.6 
+1.(-1).(-2)] 
=[-16+0-30]-[60+0+2]=-108 
= -108 
8 
§2: Định Thức 
Bài tập: Tính 
= -55 
9 
§2: Định Thức 
10 
§2: Định Thức 
Ví dụ: Cho ma trận 
11 
§2: Định Thức 
Bài tập: Với 
Tính 
12 
§2: Định Thức 
13 
§2: Định Thức 
14 
§2: Định Thức 
Ví dụ: Tính định thức sau: 
15 
§2: Định Thức 
Ví dụ: Tính định thức sau: 
= -18-2(-52) = 86 
16 
§2: Định Thức 
Ví dụ: Tính định thức sau: 
17 
§2: Định Thức 
Bµi TËp: TÝnh ®Þnh thøc sau 
= 102 
18 
§2: Định Thức 
TÝnh chÊt cña ®Þnh thøc 
19 
§2: Định Thức 
VÝ dô: 
20 
§2: Định Thức 
21 
§2: Định Thức 
VÝ dô: 
22 
§2: Định Thức 
23 
§2: Định Thức 
24 
§2: Định Thức 
VÝ dô: 
25 
§2: Định Thức 
26 
§2: Định Thức 
VÝ dô: 
27 
§2: Định Thức 
 (5) Nếu nhân mỗi phần tử của hàng thứ i với cùng một số rồi cộng vào hàng k thì định thức không đổi 
28 
§2: Định Thức 
VÝ dô: 
29 
§2: Định Thức 
30 
§2: Định Thức 
Ví dụ: 
31 
§2: Định Thức 
32 
§2: Định Thức 
Ví dụ: 
33 
§2: Định Thức 
	Dùng các tính chất của định thức để 
tính định thức: 
	 Phương pháp: Dùng các phép biến đổi có 
dạng sau 
ta đưa định thức đã cho về dạng tam giác. 
34 
§2: Định Thức 
Ví dụ: Tính định thức 
35 
§2: Định Thức 
36 
§2: Định Thức 
Hay 
37 
§2: Định Thức 
Bài tập: Tính định thức 
38 
§2: Định Thức 
Bài tập: Tính định thức sau 
= ? 
39 
§2: Định Thức 
Ví dụ: Tính định thức cấp n sau 
Tiếp tục hàng 3 trừ hàng 1, hàng 4 trừ hàng 1,  
40 
§2: Định Thức 
Ta được: 
41 
§2: Định Thức 
42 
§2: Định Thức 
Ví dụ: Cho 2 ma trận