Bài giảng Cơ học lý thuyết - Tuần 3 - Nguyễn Duy Khương

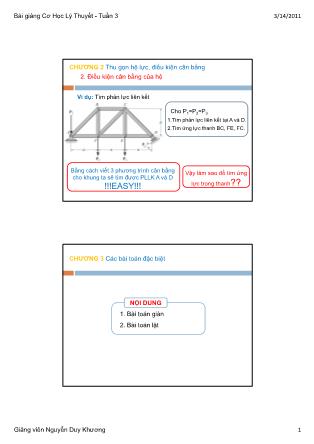
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 1
CHƯƠNG 2 Thu gọn hệ lực, điều kiện cân bằng
2. Điều kiện cân bằng của hệ
Ví dụ: Tìm phản lực liên kết
1.Tìm phản lực liên kết tại A và D.
Cho P1=P2=P3
2.Tìm ứng lực thanh BC, FE, FC.
Bằng cách viết 3 phương trình cân bằng 
cho khung ta sẽ tìm được PLLK A và D 
!!!EASY!!!
Vậy làm sao để tìm ứng 
lực trong thanh??
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
2. Bài toán lật
NỘI DUNG
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 2
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
Một số dạng giàn
Giàn Không Phải 
Giàn
Giàn
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
Bài toán giàn ta có thể tìm
thấy trong xây dựng như
cầu, khung nhà, khung sân
khấu, khán đài
Một số dạng kết cấu giàn
thông dụng:
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 3
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
Ứng lực bên trong thanh giàn
Kéo
Nếu ứng lực dương thanh chịu kéo
Nếu ứng lực âm thanh chịu nén
Bài toán thanh là bài toán mà thanh chỉ chịu lực 
kéo hoặc nén ở hai đầu
Nén
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
1
2
3
4
A
Ứng lực bên trong thanh giàn
S1
S2
S3
S4
S1
S2
S3
S4
S1>0 : hướng vào thanh
S2<0 : hướng ra khỏi thanh
S3<0 : hướng ra khỏi thanh
S4>0 : hướng vào thanh
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
Để giải các loại bài toán thanh giàn ta có các cách giải sau:
2. Phương pháp mặt cắt
3. Phương pháp đồ thị
4. Phương pháp Maxoen-Cremona
1. Phương pháp tách nút
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
1. Phương pháp tách nút
Ta xét lần lượt từng nút sao cho tại mỗi nút chỉ còn 2 ẩn để ta có
thể giải, vì xét tại mỗi nút là hệ lực đồng quy nên chỉ có 2 phương
trình cân bằng.
Với bài toán bên ta lần lượt làm
các bước sau
1. Xét nguyên khung cân bằng tìm
phản lực liên kết
2. Xét nút A cân bằng AB
S
AFS
xA
yA 1
P
A
3. Xét nút B cân bằng B BCS
BFS
BA ABS S 
4. Xét các nút còn lại sao cho số ẩn là 2 ẩn
-Lập 2 pt 2 ẩn
-Lập 2 pt 2 ẩn
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 5
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
Ví dụ: Cho hệ giàn như hình vẽ, biết thanh 1, 3, 4, 6, 8, 9 có độ 
dài a=1m, F1=F2=F3=3T.
a) Tìm phản lực liên kết tại A và B.
b) Tìm ứng lực trong tất cả các thanh.
Giải
F3 8 9
5 6
7
3
4
1 245
0
F2
F1 A
B
C D
E F
Bậc tự do hệ: 3 9 2 1 12 2 0dof 
a) Tìm phản lực liên kết tại A và B
Hóa rắn vật, giải phóng liên kết tại A và B:
F3
F2
F1 A
B
C
D
E F
Ay
By
Bx
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
Điều kiện hệ thanh cân bằng
F3
F2
F1 A
B
C
D
E F
Ay
By
Bx 1 2 3
1 2
0
0
2 2 0
x
y
yB
x
yyA
A
F F F F
F B
M a F F
B
a a

9
2
9
9
2
y
x
y
B
B
T
T
T
A 
b) Tìm ứng lực trong các thanh
Tách vật, xét từng nút sao cho tại nút đang xét có 2 ẩn số.
•Xét nút A cân bằng:
A
F1
Ay
S1
S2
(hệ lực đồng quy có 2 phương trình cân bằng)
2
1 2
1
2 0
2
2 0
2
x
y y
F F
F A
S
S S


1
2
3
2
3 2
S
S
T
T
(Thanh 1 
và 2 chịu 
lực nén)
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 6
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
•Xét nút C cân bằng:
C
F2
S1
S4
S3
3
4
2
1
0
0
x
y
F S
S
F
F S

3
4
3
3
2
S
S
T
T
•Xét nút E cân bằng:
EF3
S4 S5
S8
8 5
5
3
4
2 0
2
2 0
2
x
y
F S S
F S
F
S


5
8
3 2
2
9
2
S T
TS
•Xét nút F cân bằng:
F
S6
S9
S8 8 9
6
0
0
x
y
F S
F
S
S

6
9
0
9
2
T
S
S
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
•Xét nút B cân bằng:
B
7
7
9
2 0
2
2 0
2
x x
y y
S
S
F B S
F B


S9
By
Bx
S7
7
7
9 2
2
9 2
2
S
S
T
T
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 7
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
B C
2. Phương pháp mặt cắt
Ta sử dụng mặt cắt cắt qua 3 thanh bất kì chia giàn thành 2 khung
riêng, sau đó ta chỉ cần xét cân bằng cho 1 bên để tìm ứng lực.
Với bài toán bên ta lần lượt làm các
bước sau:
1. Xét khung cân bằng tìm
phản lực liên kết (3 phương
trình)
2. Cắt ngang 3 thanh mà ta
muốn tính ứng lực (3
phương trình)
JIS
JDS
CDS
xA
yA
1F 2F
CHƯƠNG 3 Các bài toán đặc biệt
1. Bài toán giàn
F3 8 9
5 6
7
3
4
1 245
0
F2
F1 A
B
C D
E F Tìm ứng lực trong thanh 3 và 4
F3
F2
F1 A
B
C
D
E F
Ay
By
Bx
S3
S2
S4
Xét thanh AC cân bằng
1 2 2 3
2
2
4
3
2 0
2
2 0
2
0
x
y y
A
S S
S
F F F
S
F A
M a F
S
a



3
4
2 3 2
3
3
2
S
S
T
T
T
S
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 8
CHƯƠNG 3 Các bài toán đặc biệt
2. Bài toán lật
Điều kiện để vật không bị lật lat chonglatM M 
Để làm những dạng bài này ta chỉ cần tính
moment lật và moment chống lật rồi thế vào
bất đẳng thức
Tìm khối lượng của tháp nước để tháp 
không bị lật?
A B
q
P
CHƯƠNG 3 Các bài toán đặc biệt
2. Bài toán lật
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 9
CHƯƠNG 4 Ma sát
1. Các lực ma sát và tính chất của chúng
2. Bài toán cân bằng có kể đến ma sát
NỘI DUNG
CHƯƠNG 4 Ma sát
1. Các lực ma sát và tính chất của chúng
Hai vật tựa lên nhau, cản trở chuyển động hay xu hướng chuyển
động tương đối của vật này lên bề mặt của vật kia, ở chỗ tiếp
xúc gọi là ma sát.
Trong nhiều trường hợp ta muốn giảm thiểu mức độ ảnh hưởng
của lực ma sát
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 10
CHƯƠNG 4 Ma sát
1. Các lực ma sát và tính chất của chúng
Trong nhiều trường hợp ta muốn tăng tối đa mức độ ảnh hưởng
của lực ma sát
CHƯƠNG 4 Ma sát
1. Các lực ma sát và tính chất của chúng
Khi hai vật trượt lên nhau, lực ma sát chính là nguyên nhân
dẫn đến tổn thất năng lượng và năng lượng tổn thất sẽ biến
thành nhiệt và sự ăn mòn của vật liệu.
Các loại ma sát:
+Ma sát khô (Dry Friction): Khi hai bề mặt vật rắn tiếp xúc và
trượt lên nhau. Lực ma sát tiếp tuyến với bề mặt tiếp xúc.
+Ma sát nhớt (Fluid Friction): Ma sát nhớt sinh ra khi các lớp
của lưu chất chuyển động với vận tốc khác nhau.
+Ma sát nội (Internal Friction): Khi ta tác động lực lên vật rắn
làm vật đó biến dạng thì các phần tử bên trong chuyển động
tương đối với nhau sinh ra ma sát giữa các phần tử gọi là ma
sát nội.
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 11
CHƯƠNG 4 Ma sát
1. Các lực ma sát và tính chất của chúng
MA SÁT KHÔ
Có hai loại ma sát trong ma sát khô:
1. Ma sát tĩnh: hai bề mặt tiếp xúc đứng yên tương đối với nhau
2. Ma sát động: hai bề mặt tiếp xúc chuyển động tương đối với
nhau
CHƯƠNG 4 Ma sát
1. Các lực ma sát và tính chất của chúng
MA SÁT TĨNH
Lực ma sát tĩnh có giá trị từ 0 Fmax , kết
quả lực ma sát tĩnh được tính từ phương
trình cân bằng.
max tF N 
Điều kiện để vật chưa trượt là maxms tF F N 
Với N là phản lực giữa hai bề mặt tiếp xúc
là hệ số ma sát tĩnht
Lưu ý: Lực ma sát không phụ thuộc vào diện 
tích bề mặt tiếp xúc
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 12
CHƯƠNG 4 Ma sát
1. Các lực ma sát và tính chất của chúng
MA SÁT ĐỘNG
1. Ma sát trượt: hai bề mặt tiếp xúc trượt lên nhau.
Có hai loại ma sát trong ma sát động:
Khi lực ma sát vượt qua giới hạn tĩnh vật sẽ chuyển động, lúc đó
ma sát giữa hai bề mặt là ma sát động.
Lực ma sát trượt giữa hai bề mặt là:
k kF N 
Với là hệ số ma sát trượtk
Nhận xét: lực ma sát trượt thường
nhỏ hơn lực ma sát tĩnh
CHƯƠNG 4 Ma sát
1. Các lực ma sát và tính chất của chúng
Góc ma sát
maxF
msF
R 'R
maxtan t
F
N
  Góc ma sát giới hạn
Góc ma sát tĩnh mtan sF
N
Điều kiện để vật chưa trượt là 
N
P
T
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 13
CHƯƠNG 4 Ma sát
1. Các lực ma sát và tính chất của chúng
2. Ma sát lăn: hai bề mặt tiếp xúc lăn lên nhau.
lM
Ma sát cản lăn sinh ra là do biến dạng
đàn hồi giữa vật rắn và nền, biến dạng
càng lớn ma sát cản lăn càng cao.
maxM kN 
Với k là hệ số ma sát cản lăn, và k=a,
vậy k có thứ nguyên chiều dài phụ
thuộc vào sự đàn hồi bề mặt lăn
Điều kiện để vật chưa lăn là maxlM M kN 
Các khả năng biện luận
- Vật không lăn và không trượt
- Vật lăn và không trượt
- Vật trượt và không lăn
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
Ví dụ: Tìm góc tối đa để vật M chưa trượt, biết ma sát trượt f
sin 0
cos 0
x ms
y
F mg F
F N mg



Điều kiện cân bằng: 
sin
cos
msF mg
N mg


Để M không trượt max .msF F f N sin . cosmg f mg  
tan f 
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 14
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
Ví dụ: Vật 1 có trọng lượng P, vật 2 có trọng lượng Q, hệ số
ma sát trượt tĩnh giữa vật 1 và 2 là f, bỏ qua ma sát vật 2 với
sàn và các ma sát ròng rọc, dây không co giãn khối lượng dây
không đáng kể. Lực F tác dụng vào vật 2 theo phương ngang
như hình vẽ. Tìm lực F tối đa để vật 1 không trượt trên vật 2.
1
2
F
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
Phân tích lực tác động lên hai vật:
1
N1T
P Fms
Q
Fms
N1
N2
T
2
F
1
0
0
x
y
msT F
N
F
F P

Điều kiện cân bằng vật 1: 
Điều kiện cân bằng vật 2: 
2 1
0
0
mx
y
sF
N NQ
T
F
FF 

Lập được 4 phương trình 4 ẩn ta giải được
1
2
/ 2
/ 2ms
N
N
T
F
P
P Q
F
F
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 15
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
Điều kiện để vật 1 không trượt trên vật 2
ma 1xmsF fF N 
/ 2F fP 
2 fF P 
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
Ví dụ: Cho mô hình sau biết hệ số ma sát trượt tĩnh giữa các
vật như hình, dây không co giãn khối lượng dây không đáng
kể. Lực P tác dụng vào vật 2 theo phương như hình vẽ. Tìm
lực P tối đa để các vật đều không trượt.
Bài giảng Cơ Học Lý Thuyết - Tuần 3 3/14/2011
Giảng viên Nguyễn Duy Khương 16
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
Phân tích lực tác động lên vật:
Xét vật 1 cân bằng
1
1
30(9.81) cos(30 ) 0
30(9.81)sin(30 ) 0
o
o
N
T F
1 2
1 2
50(9.81) cos(30 ) 0
50(9.81)sin(30 ) 0
o
o
N N
FP F
3 2
2 3
40(9.81) cos(30 ) 0
40(9.81)sin(30 ) 0
o
o
N N
F F
Xét vật 2 cân bằng
Xét vật 3 cân bằng
Sáu phương trình 7 ẩn T, N1, N2, N3, F1, F2, F3.
CHƯƠNG 4 Ma sát
2. Bài toán cân bằng có kể đến ma sát
Nhận xét để hệ không trượt ta xét lực ma sát 1 ở trạng thái
chuẩn bị trượt lúc đó F1=0.3N1, vậy hệ phương trình chỉ còn 6ẩn 6 phương trình. Giải 6 ẩn (T, N1, N2, N3, F2, F3) ta được
1
2
3
2
3
255
680
1019
224
169
365
P
N
N
N
T
F P
F
Để vật không trượt thì
max 2 2
m
2
a 33 x3
0.4
0.45
F
F
F N
F N
169 272
365 459
P
P
103
94
P
P
94P 
Vậy lực P tối đa là 94N để hệ không trượt